Chapitre 2 - Dérivées et sens de variations
Dans ce chapitre, nous nous intéressons au calcul des dérivées et à l'étude de variation qui en découle.
IDérivée de fonctions
1Fonctions usuelles
On note \(f'\)la dérivée de la fonction \(f\), \(D_f\) l'ensemble de définition de la fonction \(f\) (voir fiche),
et \(D_{f'}\) l'ensemble de définition de la fonction \(f'\).
$$ \begin{array}{|c|c|c|c|} \hline f & f' & D_f & D_{f'} \\\hline \hline k\in\mathbb{R} & 0 & \mathbb{R} & \mathbb{R} \\\hline x & 1 & \mathbb{R} & \mathbb{R} \\\hline x^2 & x & \mathbb{R} & \mathbb{R} \\\hline x^3 & 3x^{2} & \mathbb{R} & \mathbb{R} \\\hline \hline \frac{1}{x} &\frac{-1}{x^2} & \mathbb{R}^{*}& \mathbb{R}^{*} \\\hline \sqrt{x} & \frac{1}{2\sqrt{x}}& \mathbb{R}^{+}&\mathbb{R}^{+*} \\\hline \end{array}
$$
- \(\mathbb{R}\) se note aussi \(]-\infty; +\infty[\)
- \(\mathbb{R^{+}}\) se note aussi \([0 ; +\infty[\)
- \(\mathbb{R^{*}}\) se note aussi \(\mathbb{R}\_\{0\}\)
2Opérations sur les fonctions dérivables
Soient \(u\) et \(v\) deux fonctions dérivables et \(k\) un nombre réel :
- \((u+v)'=u' + v'\)
- \((k u)'=k u'\)
- \((u v)'=u'v+u v'\)
- \((\frac{u}{v})'=\frac{u' v - u v'}{v^2}\)
- \((\frac{1}{v})'=\frac{- v'}{v^2}\)
3Primitive
Si \(g\) est la dérivée de \(f\), alors \(f\) est une primitive de \(g\)
Une primitive de \(f\) se note généralement \(F\)
Soit \(f (x)=2x + 1\), alors la fonction définie par \(F (x) = x^2 + x\) est une primitive de \(f\)
IISens de variations et dérivées
1Sens de variations
\(f\) est dérivable, définie sur un intervalle \(I\) :
- Si \(f'\) est positive sur \(I\), alors \(f\) est croissante sur \(I\)
- Si \(f'\) est négative sur \(I\), alors \(f\) est décroissante sur \(I\)
- Si \(f'\) est nulle sur \(I\), alors \(f\) est constante sur \(I\)
2Extremum local
On représente une fonction \(f\) ci-dessous avec \(5\) extrema :
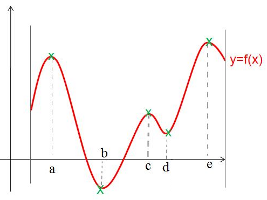
- La fonction \(f\) présente des maxima locaux en \(a\), \(c\) et \(e\)
- La fonction \(f\) présente des minima locaux en \(b\) et \(d\)
- La fonction \(f\) présente un maximum global en \(e\) et un minimum global en \(b\)
IIILien entre nombre dérivé et tangente
Le nombre dérivé a une interprétation géométrique :
Le nombre dérivée \(f '(a)\) est le coefficient directeur de la droite tangente (si elle existe) à la
courbe en \(x=a\) , c'est à dire le taux de variation entre a et b quand b se rapproche de a :
$$ f'(a) = lim \frac{f (a+h) - f (a)}{h} $$
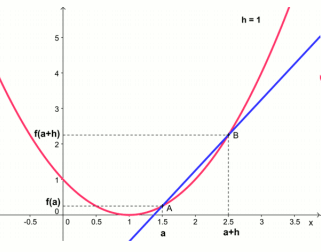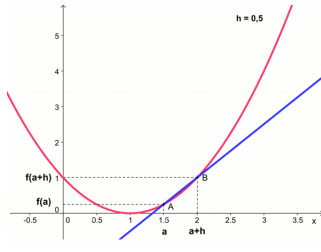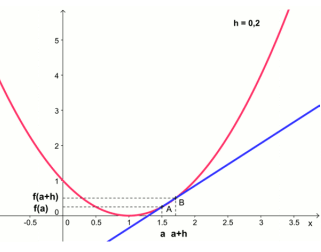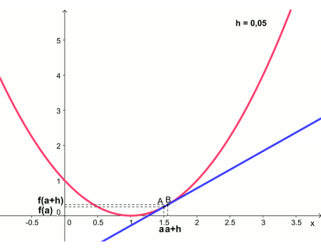
L'équation de la droite tangente \(T\) à la courbe en \(x=a\) a pour équation :
$$y=f'(a) (x - a) + f (a)$$